vastlift.blogg.se - Find the error condense logarithms

#Find the error condense logarithms how to

The next section will show you how condensing logarithms is the opposite of expanding logarithms. For example: logb(6x y) logb(6x)logby logb6+logbxlogby l o g b ( 6 x y) l o g b ( 6 x) l o g b y l o g b 6 + l o g b x l o. Sometimes we apply more than one rule in order to expand an expression.

#Find the error condense logarithms how to

Learn how to apply the different logarithmic rules and properties. Taken together, the product rule, quotient rule, and power rule are often called properties of logs.

1 log66 1 Exercise 7.4.1 Evaluate using the properties of logarithms: log131 log99 Answer Exercise 7.4. log( a2 b3)+log(c)log(d4) log ( a 2 b 3) + log ( c) - log ( d 4) Use the product property of logarithms, logb(x)+ logb(y) logb(xy) log b ( x) + log b ( y) log b ( x y). Evaluate using the properties of logarithms: log81 log66 Solution: a. Check out all of our online calculators here log2 ( 18) log2 ( 3) Go. Practice your math skills and learn step by step with our math solver.

Refresh the difference between common and natural logarithms. Use the quotient property of logarithms, logb (x)logb(y) logb( x y) log b ( x) - log b ( y) log b ( x y). Condensing Logarithms Calculator Get detailed solutions to your math problems with our Condensing Logarithms step-by-step calculator.

Make sure to review the different parts and fundamental definitions of logarithms.

This article makes use of various concepts we’ve learned in the past, so make sure to review these topics on logarithms before diving right into our main topic – condensing logarithms. This helps us simplify expressions size-wise and save space by combining the expressions that share common bases.Ĭondensing logarithmic expressions is the process of using different logarithmic properties to combine different logarithmic terms into one quantity. We'll take on some gruesome expressions that involve logs and learn to write the expressions as a single logarithm.Condensing Logarithms – Properties, Explanation, and ExamplesĬondensing logarithms are helpful when we’re given a long logarithmic expression haring similar bases. It's time to get back to mathematics and try simplifying logs using concrete formulas.

Quite a few physical units are based on logarithms, for instance, the Richter scale, the pH scale, and the dB scale.Īlright, that should be enough of a description for now.

Chemistry, e.g., the half-life decay and.

Medicine, e.g., the Quantitative Insulin Sensitivity Check Index (QUICKI).

Statistics, e.g., the lognormal distribution.

where possible, evaluate logarithmic expressions.

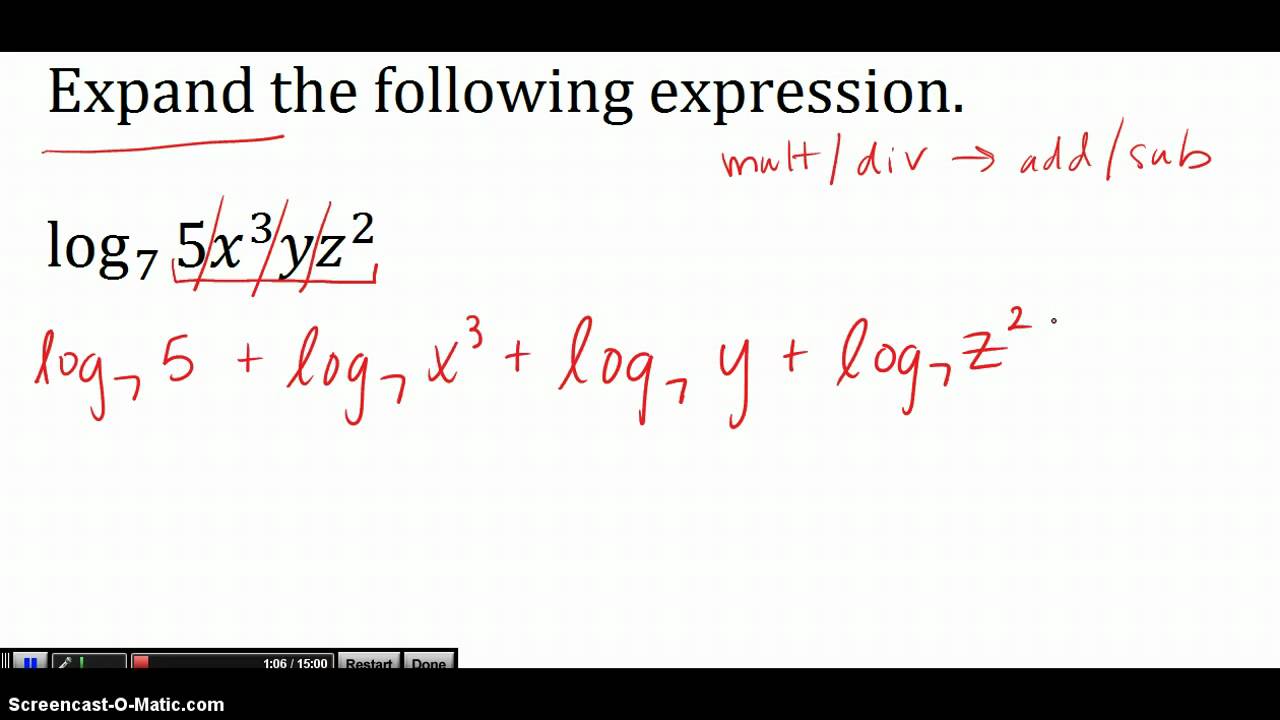
write the expression as a single logarithm whose coefficient is 1. After all, whatever we raise to power 0 0 0, we get 1 1 1. Use properties of logarithms to condense the logarithmic expression below. We can use the rules of logarithms we just learned to condense sums, differences, and products with the same base as a single logarithm. Whatever the base, the logarithm of 1 1 1 is equal to 0 0 0. In other words, whenever we write log ⁡ a b \log_a b lo g a b, we require b b b to be positive. Solve - Simplifying logarithms calculator Get it on Google Play Get it on Apple Store Solve Simplify Factor Expand Graph GCF LCM Solve an equation, inequality or a system. The logarithm function is defined only for positive numbers. If you're curious, log base 2 calculator is the way to go. What causes condensation to occur and how can you deal with it Find out how to avoid condensation and dampness with improved ventilation and insulation. There is also the binary logarithm, i.e., log with base 2 2 2, but it's not as common as the first two. The former is denoted ln ⁡ x \ln x ln x and its base is the Euler number - you can read more about it in the natural log calculator! The latter is denoted log ⁡ x \log x lo g x with the base being (surprise, surprise!) the number 10 10 10. There are two very special cases of the logarithm which have unique notation: the natural logarithm and the logarithm with base 10 10 10. Before we learn how to rewrite logs, let's mention a few critical facts concerning them.